solución de ejercicios

Solución del ejercicio 1

Calcular todos los múltiplos de 17 comprendidos entre 800 y 860.

Para calcular el primer múltiplo de 17 tomamos el siguiente número entero que resulta de dividir 800 entre 17 y lo multiplicamos por 17.

48 · 17 = 816.

49 · 17 = 833.

50 · 17 = 850.

816, 833, 850

Solución del ejercicio 2

De los siguientes números: 179, 311, 848, 3566, 7287. Indicar cuáles son primos y cuáles compuestos.

Primos: 179 y 311.

Compuestos: 848, 3566 y 7287.

Solución del ejercicio 3

Calcular, mediante una tabla, todos los números primos comprendidos entre 400 y 450.

	401								409
									419
	421
	431		433						439
			443						449

Descomponer en factores

1 216

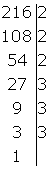
216 = 2³ · 3³

2 360

360 = 2³ · 3² · 5

3 432

432 = 2⁴ · 3³

Solución del ejercicio 5

Factorizar 342 y calcular su número de divisores.

342 = 2 · 3² · 19

Nd = (1 + 1) · (2 + 1) · (1 + 1) = 12

Solución del ejercicio 6

Descomponer en factores

1 2250

2250 = 2 · 3² · 5³

2 3500

3500 = 2² · 5³ · 7

3 2520

2 520 = 2³ · 3² · 5 · 7

Solución del ejercicio 7

Calcular el m. c. d. y m.c.m. de:

1 428 y 376

428 = 2² · 107

376 = 2³ · 47

m. c. d. (428, 376) = 2² = 4

m. c. m. (428, 376) = 2³ · 107 · 47 = 40 232

2 148 y 156

148 = 2² · 37

156 = 2² · 3 · 13

m. c. d. (148, 156) = 2² = 4

m. c. m. (148, 156) = 2² · 3 · 37 · 13 = 5772

3 600 y 1 000

600 = 2³ · 3 · 5²

1 000 = 2³ · 5³

m. c. d. (600, 1 000) = 2³ · 5² = 200

m. c. m. (600, 1 000) = 2³ · 3 · 5³ = 3000

Solución del ejercicio 8

Calcular el m. c. d. y m.c.m. de:

1 72, 108 y 60.

72 = 2³ · 3²

108 = 2² · 3³

60 = 2² · 3 · 5

m.c.d. (72, 108, 60) = 2² · 3 = 12

m. c. m. (72, 108, 60) = 2³ · 3³ · 5 = 1080

2 1048, 786 y 3930

1048 = 2³ · 131

786 = 2 · 3 · 131

3930 = 2 · 3 · 5 · 131

m. c. d. (1048, 786, 3930) = 2 · 131 = 262

m. c. m. (1048, 786, 3930) = 2³ · 3 · 5 · 131 = 15 720

3 3120, 6200 y 1864

3210 = 2⁴ · 3 · 5 · 13

6200 = 2³ · 5² · 31

1864 = 2³ · 233

m. c. d. (3210, 6200, 1864) = 2³ = 8

m. c. m. (3210, 6200, 1864) = 2⁴ · 3 · 5² · 13 · 31 · 233 =

= 112 678 800

Solución del ejercicio 9

Calcular por el algoritmo de Euclides, el m.c.d. de:

1 72, 16

m. c. d. (72, 16) = 8

2 656 y 848

m.c.d.(656, 848) = 16

3 1728 y 842

m.c.d. (1278, 842) = 2